BLAS

https://www.cs.utexas.edu/users/flame/pubs/GotoTOMS_final.pdf

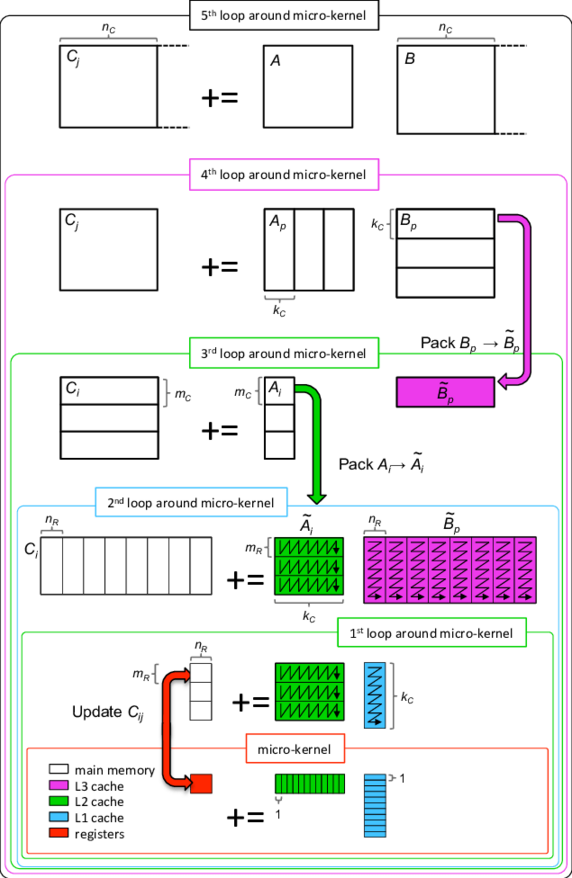
A 为 M x K, B 为 K x N

1. A, B 拆分成较小的 A' (M_c x K_c) 和 B' (K_c x N_c), A' 在 l2 cache, B'在 l3 cache
2. A', B' 拆分为更小的 A'' (M_r x K_c) 和 B'' (K_c x N_r), B'' 在 l1 cache, M_r/N_r 的典型值为 2
3. 计算 A'' x B'' 时使用了 `列 dot 行`的形式 , 所以 A' 需要以 M_r 为单位纵向 pack, B' 需要以 N_r 为单位横向 pack, 以便读数据时能利用 l1 cache

• K_c 和 N_c 取决于 l3 cache
• K_c 和 M_c 取决于 l2 cache
• K_c 和 M_r, N_r 取决于 l1 cache

openblas 使用 GEBP 类型的 kernel, N_c 通常较大, 例如 4K. M_c/K_c 较小, 例如 128/256.

假设 M_c=N_c=K_c = 4, M_r=N_r=2, openblas pack 的结果为:

pack 之前:

A': (矩阵的值, 非内存中的布局)

0.170828 0.577304 0.873904 0.732520
0.749902 0.785799 0.745095 0.260222
0.096372 0.692194 0.446046 0.394294
0.870465 0.368766 0.353728 0.776790

B':

0.845035 0.455825 0.568585 0.275509
0.575788 0.109947 0.959066 0.260361
0.715539 0.545228 0.867719 0.924095
0.083004 0.390687 0.163190 0.435923

pack 之后:

A'':

(gdb) x /8fg ba
0x7fffefd7d000: 0.17082803610628972     0.74990198048496381
0x7fffefd7d010: 0.57730350679510778     0.78579925883967405
0x7fffefd7d020: 0.87390407686180893     0.74509509845006505
0x7fffefd7d030: 0.73251963200253911     0.26022200108288018

B'':

(gdb) x /8fg bb
0x7fffefd9d000: 0.84503513758028603     0.45582512865975744
0x7fffefd9d010: 0.57578820048277635     0.10994681418064545
0x7fffefd9d020: 0.71553859516866325     0.54522802381657343
0x7fffefd9d030: 0.083004246073876686    0.39068657064867551

openblas SGEMMKERNEL 计算的是 packed A' x packed B', 所以 gemm kernel 需要先通过 SGEMMONCOPY/SGEMMOTCOPY 进行 pack, 且 COPY 和 SGEMMKERNEL 需要对应相同的 M_r/N_r, 否则数据的布局会对应不上.

openblas 中的 param.h 中定义了以上几个值:

• SGEMM_DEFAULT_P 对应 M_c
• SGEMM_DEFAULT_Q 对应 K_c
• SGEMM_DEFAULT_R 对应 N_c
• SGEMM_DEFAULT_UNROLL_M 对应 M_r
• SGEMM_DEFAULT_UNROLL_N 对应 N_r

以 gemmkernel_2x2.c 为例:

int CNAME(
    BLASLONG bm, BLASLONG bn, BLASLONG bk, FLOAT alpha, IFLOAT* ba, IFLOAT* bb,
    FLOAT* C, BLASLONG ldc) {
    BLASLONG i, j, k;
    FLOAT *C0, *C1;
    IFLOAT *ptrba, *ptrbb;
    FLOAT res0, res1, res2, res3;
    IFLOAT load0, load1, load2, load3, load4, load5, load6, load7;
    /* NOTE: ba 即 packed A', bb 则 packed B' */
    /* NOTE: bn 即 N_c, /2 表示 N_r 为 2 */
    for (j = 0; j < bn / 2; j += 1) {
        C0 = C;
        C1 = C0 + ldc;
        /* NOTE: ptrba 相当于 A'' */
        ptrba = ba;
        for (i = 0; i < bm / 2; i += 1) {
            /* NOTE: bm 即 M_c, M_r=2 */
            /* NOTE: ptrbb 相当于 B'' */
            ptrbb = bb;
            res0 = 0;
            res1 = 0;
            res2 = 0;
            res3 = 0;
            /* NOTE: bk 即 K_c, /4 表示计算 A'' x B'' 时针对 K_c 循环展开 4 次
             */
            for (k = 0; k < bk / 4; k += 1) {
                /* NOTE: 计算 A'' x B'', 每次得到 4 个值 (因为每次 A'' 的一列
                 * dot B'' 的一行, 结果为 2x2 矩阵") */
                load0 = ptrba[2 * 0 + 0];
                load1 = ptrbb[2 * 0 + 0];
                res0 = res0 + BF16TOF32(load0) * BF16TOF32(load1);
                load2 = ptrba[2 * 0 + 1];
                res1 = res1 + BF16TOF32(load2) * BF16TOF32(load1);
                /* ... */
                ptrba = ptrba + 8;
                ptrbb = ptrbb + 8;
            }
            /* NOTE: 循环展开时 K_c 不能被 4 整除 */
            for (k = 0; k < (bk & 3); k += 1) {
                load0 = ptrba[2 * 0 + 0];
                load1 = ptrbb[2 * 0 + 0];
                /* ... */
            }
            res0 = res0 * alpha;
            C0[0] = C0[0] + res0;
            res1 = res1 * alpha;
            /* ... */
            C0 = C0 + 2;
            C1 = C1 + 2;
        }
        /* NOTE: M_c 不能被 2 整除 */
        for (i = 0; i < (bm & 1); i += 1) {
            ptrbb = bb;
            res0 = 0;
            res1 = 0;
            for (k = 0; k < bk; k += 1) {
                load0 = ptrba[0 + 0];
                load1 = ptrbb[2 * 0 + 0];
                res0 = res0 + BF16TOF32(load0) * BF16TOF32(load1);
                /* ... */
            }
            res0 = res0 * alpha;
            /* ... */
            C1 = C1 + 1;
        }
        k = (bk << 1);
        bb = bb + k;
        i = (ldc << 1);
        C = C + i;
    }
    /* NOTE: N_c 不能被 2 整除 */
    * / for (j = 0; j < (bn & 1); j += 1) {
        C0 = C;
        ptrba = ba;
        for (i = 0; i < bm / 2; i += 1) {
            ptrbb = bb;
            res0 = 0;
            res1 = 0;
            for (k = 0; k < bk; k += 1) {
                load0 = ptrba[2 * 0 + 0];
                load1 = ptrbb[0 + 0];
                res0 = res0 + BF16TOF32(load0) * BF16TOF32(load1);
                /* ... */
            }
            res0 = res0 * alpha;
            C0[0] = C0[0] + res0;
            /* ... */
        }
        for (i = 0; i < (bm & 1); i += 1) {
            ptrbb = bb;
            res0 = 0;
            /* ... */
        }
        k = (bk << 0);
        bb = bb + k;
        C = C + ldc;
    }
    return 0;
}

以 sgemm_kernel_16x4_c910v.c 为例, 最内层 micro kernel 需要计算 k_c 个 `(16 x 1) x (1 x 4)`, 针对 k_c 同样使用循环展开, 针对 (16 x 1) x (1 x 4), 则使用如下的计算方法:

// A: 16x1  B: 1x4

[1
 2
 3
 4    x   [a b c d]
 .
 .
 16]


// 使用 v16~v31 保存计算结果, 因为结果为 16x4

v0 = [1, 2, 3, 4]
v1 = [a, a, a, a]
v16 += v0*v1
v2 = [5, 6, 7, 8]
v17 += v0*v2
...
v0 = [13, 14, 15, 16]
v1 = [d, d, d, d]
v31 += v0*v1

计算 k_c 次后保存 v16~v31 到 c 矩阵

最简单的 gemm 实现如下所示:

for (int m = 0; m < M; m++) {
    for (int n = 0; n < N; n++) {
        for (int k = 0; k < K; k++) {
            C[m, n] += A[m, k] * B[k, n];
        }
    }
}

实际上三重循环的顺序可以任意调换, 不影响计算结果, 例如:

for (int n = 0; n < N; n++) {
    for (int m = 0; m < M; m++) {
        for (int k = 0; k < K; k++) {
            C[m, n] += A[m, k] * B[k, n];
        }
    }
}

但它们的性能并不相同.

假设 A/B/C 均为 column major, 则访问 A[m,k] 相当于 A[k*M+m], 所以从 locality 的角度出发, 遍历时我们应尽量改动 m 而不是 k.

例如:

C[m, n] += A[m, k] * B[k, n];

• m: 两次出现在 M[x,y] 的 x 位置 (C[m,n], A[m,k])
• k: 一次出现在 x 位置, 一次出现在 y 位置
• n: 两次出现在 y 位置

因此对于 column major 的 gemm, 最佳的三重循环的写法是 nkm 形式, 即:

for (int n = 0; n < N; n++) {
    for (int k = 0; k < K; k++) {
        for (int m = 0; m < M; m++) {
            C[m, n] += A[m, k] * B[k, n];
        }
    }
}

使用 blislab 的测试的结果:

# nkm
~/source/blislab/step0> sudo perf stat -e L1-dcache-loads,L1-dcache-load-misses, \
                                                            L1-dcache-stores,cycles,instructions,branches \
                                                            test/test_bl_dgemm.x  1000 1000 1000
 1000     1000    1000    2.10     inf

 Performance counter stats for 'test/test_bl_dgemm.x 1000 1000 1000':

     3,049,074,610      L1-dcache-loads                                               (83.17%)
       126,865,835      L1-dcache-load-misses     #    4.16% of all L1-dcache accesses  (83.17%)
     1,029,504,921      L1-dcache-stores                                              (83.35%)
     2,169,687,341      cycles                                                        (67.14%)
     8,171,486,214      instructions              #    3.77  insn per cycle           (83.57%)
     1,031,403,187      branches                                                      (83.17%)

       0.999021070 seconds time elapsed

       0.982300000 seconds user
       0.016037000 seconds sys

# mkn
~/source/blislab/step0#> sudo perf stat -e L1-dcache-loads,L1-dcache-load-misses, \
                                                            L1-dcache-stores,cycles,instructions,branches \
                                                            test/test_bl_dgemm.x  1000 1000 1000
 1000     1000    1000    0.17     inf

 Performance counter stats for 'test/test_bl_dgemm.x 1000 1000 1000':

     3,057,403,526      L1-dcache-loads                                               (83.34%)
     2,448,489,282      L1-dcache-load-misses     #   80.08% of all L1-dcache accesses  (83.33%)
     1,033,077,016      L1-dcache-stores                                              (83.33%)
    25,482,801,053      cycles                                                        (66.67%)
     9,233,529,254      instructions              #    0.36  insn per cycle           (83.33%)
     1,038,037,398      branches                                                      (83.33%)

      11.616521657 seconds time elapsed

      11.582296000 seconds user
       0.027986000 seconds sys

使用 blislab 的 test_bl_dgemm.c 在 skylakex 平台上测试, 大致的 benchmark 数据为:

1. 原始的 nkm 循环是 1 gflops
2. openblas 的 generic 实现 (使用 gotoblas 的拆分方法以利用 cache) 是 4 gflops
3. openblas 的 simd 实现是 20 gflops

以 sgemm_ 为例:

int sgemm_(
    char *transa, char *transb, integer *m, integer *n, integer *k, real *alpha,
    real *a, integer *lda, real *b, integer *ldb, real *beta, real *c,
    integer *ldc)