Metrics

https://en.wikipedia.org/wiki/Confusion_matrix

• P

  positive, 即 ground truth 中的真值, 或者叫 real positive

• N

  negtive, ground truth 中的假值, 或者叫 real negative

• T

  true, 即预测为 true

• F

  false, 即预测为 false

• TP

  true positive. 预测为真 (true), ground truth 为真 (positive)

• FP

  false positive. 预测为真 (true), ground truth 为假 (negative)

• TN

  true negative, 预测为假 (false), ground truth 也为假 (negative)

• FN

  false negative, 预测为假 (false), ground 为值 (positive)

• Precision

  查准率

  \(\frac{TP}{TP+FP}\) 或 \(\frac{TP}{T}\)

  即 预测正确的正样本/预测的正样本

• TPR

  true positive rate, 或者叫 recall (召回率), 查全率.

  \(\frac{TP}{TP+FN}\) 或 \(\frac{TP}{P}\)

  即 预测正确的正样本/真正的正样本

• FPR

  false positive rate

  表示 ground truth 中的 假值被预测错误 的比例

  \(\frac{FP}{FP+TN}\) 或 \(\frac{FP}{N}\)

• FNR

  false negative rate

  \(\frac{FN}{FN+TP}\) 或 \(\frac{FN}{P}\)

• TNR

  true negative rate

  \(\frac{TN}{TN+FP}\) 或 \(\frac{TN}{N}\)

• FRR

  false reject rate, 即 FNR

• FAR

  false accept rate, 即 FPR

• EER

  equal error rate.

  通过调整 threshold 使 FAR 与 FRR 相等, 这时的 FAR 或 FRR 称为 EER.

  这个值与 ROC 曲线有点关系:

  ROC 的 x 轴是 FPR, y 为 TPR. 由于 TPR = 1-FNR, 所以 fnr-fpr 曲线的形状会类似于 \(y=\frac{1}{x}\), 这个曲线与 \(y=x\) 的交点即为 EER

• Accuracy

  \(\frac{TP+TN}{P+N}\)

• F-Score

  F-Score 是 precision 和 recall 的调和平均

• ROC

  receiver operating characteristic

  当选择不同的 threshold 时, 得到不同的 FPR 和 TPR. 以 FPR 为横轴, TPR 为纵轴绘制的曲线

  这个曲线有如下的性质:

  1. x,y 坐标范围均为 [0~1]
  2. (0,0),(1,1) 必定在曲线上.
     • 当 threshold 为 0 时, 所有预测值均为真, 导致 TPR 为 1, FPR 也为 1
     • 当 threshold 为 1 时, 所有预测值均为假, 导致 TPR 为 0, FPR 也为 0
  3. 若完全随机的预测, 而 ROC 曲线 是一条连接 (0,0) 和 (1,1) 的真线

  4. 一个好的预测得到的 ROC 曲线应该在上面提供的直线的上方

     

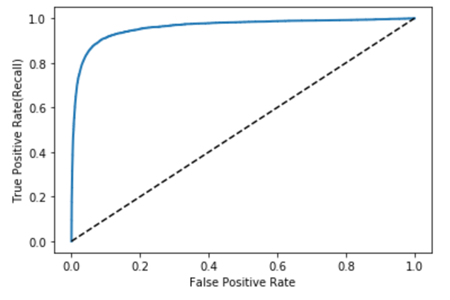
     完美的预测应该得到上图的 ROC 曲线: FPR 很低, 同时 TPR 很高, 即 ground truth 中的真值和假值都能测试正确

• AUC

  aera under the roc curve

  ROC 曲线下面围成的面积, 范围应该是 [0.5, 1]

• mAP

  precison recall curve 是选择不同的 threshold 画出 precison 和 recall 的曲线. 大约是这样:

  

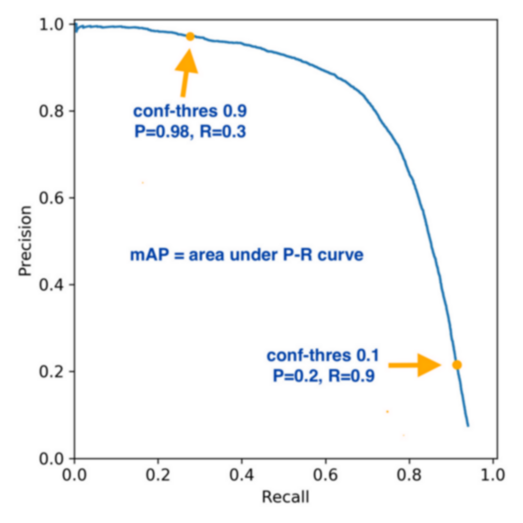
AP (average precision) 是指在 precison recall curve 上均匀的选 N 个不同的 recall, 计算其对应的 presision 的均值, 当 N 足够大时, 相当于 precision-recall 曲线的面积

mAP 是针对多个 class 的多个 AP 的均值.

AUC 和 ROC 反映 recall 和 false alarm 的关系, 而 AP 反映 recall 和 precision的关系

https://keras.io/api/metrics/classification_metrics/#truepositives-class

#!/usr/bin/env python3
import tensorflow as tf
import numpy as np
from sklearn.metrics import roc_curve, roc_auc_score
import matplotlib.pyplot as plt

y_true = np.array([0, 0, 1, 1])
y_pred = np.array([0, 0.5, 0.3, 0.9])

print("calc using sklearn")
fpr, tpr, thresholds = roc_curve(y_true, y_pred)
print(tpr, fpr, thresholds)
plt.plot(fpr, tpr)
plt.show()

print("calc using keras")
m = tf.keras.metrics.AUC(num_thresholds=3)
m.update_state(y_true, y_pred)
#
# num_thresholds 至少为 2, 对应的 threshold 为 [0,1]
# 当 num_thresholds 大于 2 时, threshold 为 [0, a,b,..., 1],  中间的 a,b,... 为
# 插值
#
# threshold values are [0, 0.5, 1]
# tp = [2, 1, 0], fp = [2, 0, 0], fn = [0, 1, 2], tn = [0, 2, 2]
# recall = [1, 0.5, 0], fp_rate = [1, 0, 0]
# auc = ((((1+0.5)/2)*(1-0))+ (((0.5+0)/2)*(0-0))) = 0.75
print("auc", m.result().numpy())
m = tf.keras.metrics.TruePositives([0, 0.5, 1])
m.update_state(y_true, y_pred)
print("tp", m.result().numpy())
m = tf.keras.metrics.FalseNegatives([0, 0.5, 1])
m.update_state(y_true, y_pred)
print("fn", m.result().numpy())

print("calc manually")
thresholds = np.array([0 - 1e-7, 0.5, 1 + 1e-7])
thresholds = np.broadcast_to(thresholds, (4, 3)).T

# tp,fp,fn,fn
tp = np.bitwise_and(y_true.astype(bool), y_pred > thresholds).sum(axis=1)
print("tp", tp)
fp = np.bitwise_and(~y_true.astype(bool), y_pred > thresholds).sum(axis=1)
tn = np.bitwise_and(~y_true.astype(bool), ~(y_pred > thresholds)).sum(axis=1)
fn = np.bitwise_and(y_true.astype(bool), ~(y_pred > thresholds)).sum(axis=1)
print("fn", fn)
# tpr,fpr
# tp+fn 即 ground truth 里有多少 true
# tpr 及 recall (查全率)
tpr = tp / (tp + fn)
# fp+tn 即 ground truth 有多少 false
fpr = fp / (fp + tn)
# precision,recall
precision = tp / (tp + fp)
recall = tpr
f_score = precision * recall / (2 * (precision + recall))

r = range(len(thresholds))
area = 0
for a, b in zip(r, r[1:]):
    area += (tpr[a] + tpr[b]) / 2 * (fpr[a] - fpr[b])

print(area)
plt.plot(fpr, tpr)
plt.show()

calc using keras auc 0.75 tp [2. 1. 0.] fn [0. 1. 2.] calc manually tp [2 1 0] fn [0 1 2] 0.75

上面提到的许多 metrics 例如 TP, FN 等都是针对 binary classification, 需要明确的 true/false 和 positive/negative.

如果是 multi-class 问题, 有两种方法有计算 metrics:

1. 把 N-class 看成 N 个 binary 问题, 针对每一个 class 计算单独的 metrics
2. 把 N-class 看成 N 个 binary 问题, 但是在计算时用某些方法来平均一下

例如:

import torch
from torchmetrics import F1Score


target = torch.tensor([0, 1, 2, 0, 1, 2])
preds = torch.tensor([0, 2, 1, 0, 0, 1])

print(F1Score(num_classes=3, average="none")(preds, target))
print(F1Score(num_classes=3, average="macro")(preds, target))
print(F1Score(num_classes=3, average="micro")(preds, target))

tensor([0.8000, 0.0000, 0.0000])
tensor(0.2667)
tensor(0.3333)

其中 `macro` 和 `micro` 使用的平均方法见参考 https://vitalflux.com/micro-average-macro-average-scoring-metrics-multi-class-classification-python/

即:

1. macro 是针对各个 class 单独计算后求平均, 比较宏观 (macro)
2. micro 是把 TP/FP 等累加后做为总的 TP/FP, 然后再依据 TP/FP 计算其它 metrics, 比较微观 (micro)